MST(Minimum Spanning Tree)란?
- 신장 트리(Spanning Tree) : 연결 그래프의 부분 그래프로서, 모든 정점과 간선의 부분 집합으로 구성 되는 트리이다. 모든 노드는 적어도 하나의 간선에 연결되어 있어야 한다.
- 최소 신장 트리(Minimum Spanning Tree) : 트리를 구성하는 간선들의 가중치를 합한 것이 최소가 되는 신장 트리이다.
- 트리의 정의에 알맞게 사이클(Cycle)이 존재하면 안된다.
크루스칼 알고리즘 (Kruskal's Algorithm)
방향성이 없는 가중치 그래프에서 최소 신장 트리를 찾는 대표적인 그리디 알고리즘이다.
동작 방식
- 첫번째로, 모든 간선을 가중치를 기준으로 오름차순 정렬한다.
- 가장 낮은 가중치의 간선을 선택하고, 신장 트리에 추가한다. 만약 해당 간선으로 인해 사이클이 형성 된다면, 해당 간선을 무시한다.
- 위 과정을 모든 노드에 닿을 때까지 반복하면, 최소 신장 트리가 만들어진다.
- 시간 복잡도는 O(ElogV)이다.
실제 예시를 통해 어떻게 동작하는지 보자.
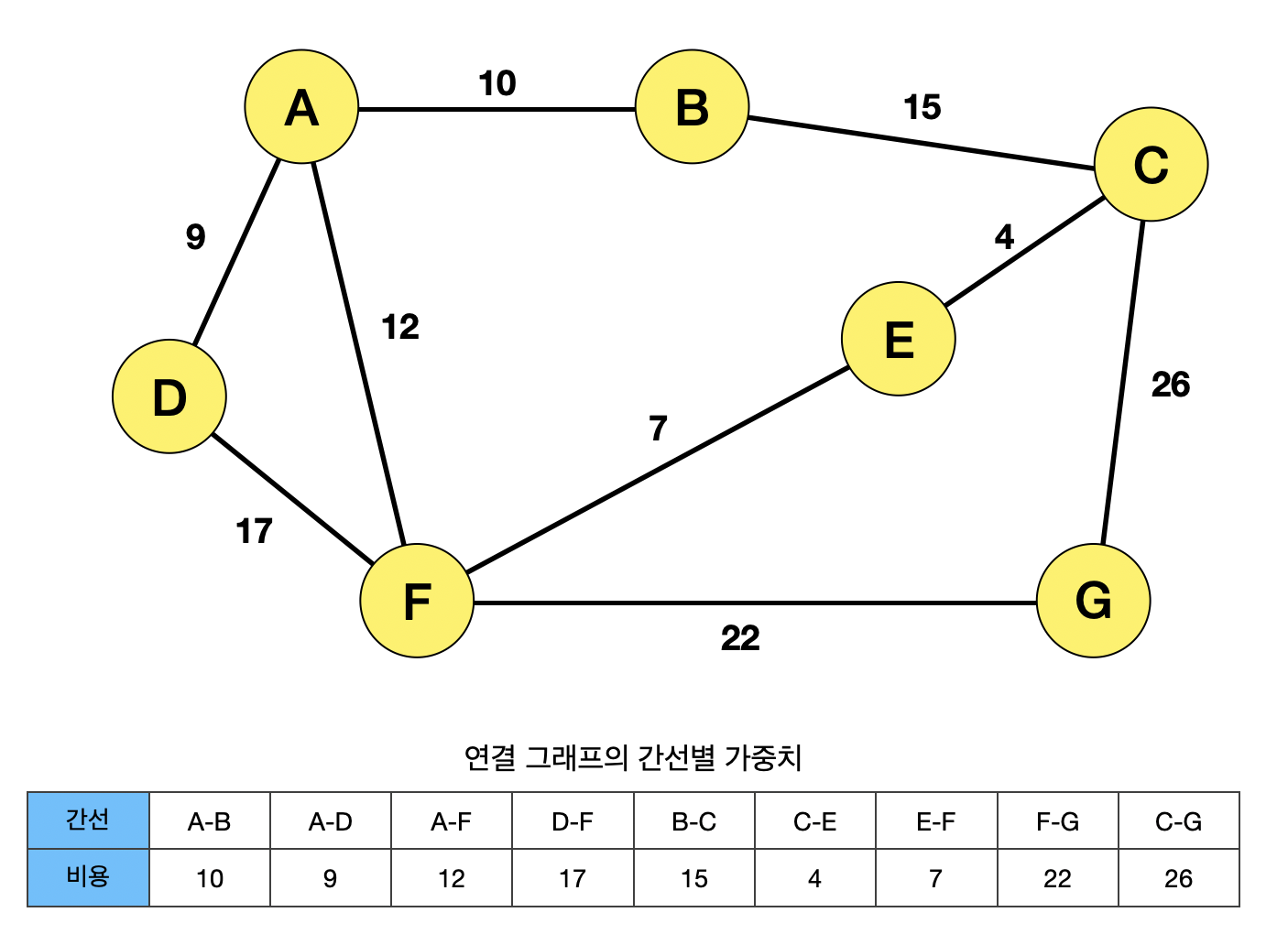
이러한 그래프가 현재 존재한다. 동작 방식 첫번째에 따라, 모든 간선을 가중치를 기준으로 오름차순 정렬한다.
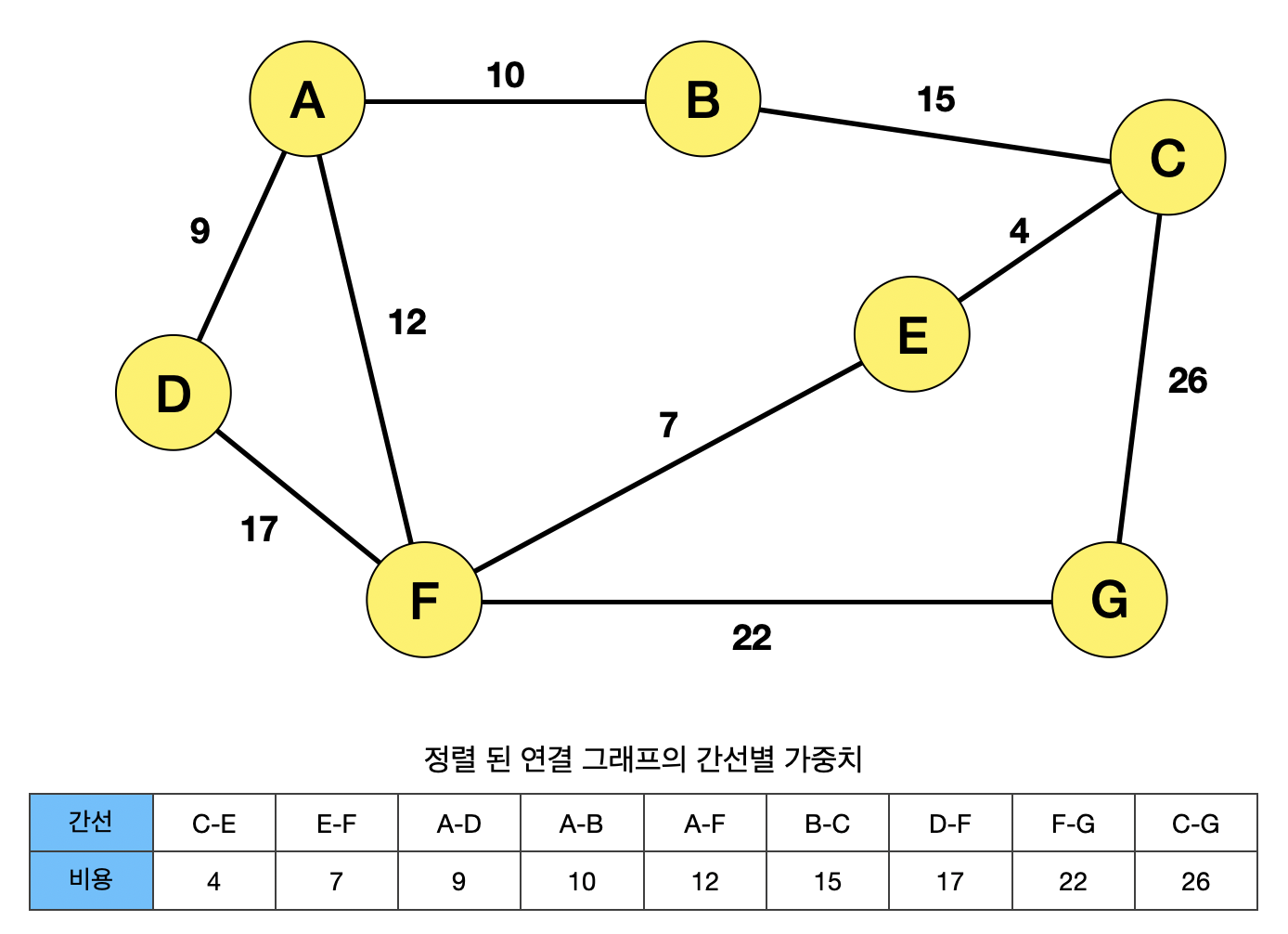
다음으로, 동작 방식 두번째에 따라, 가장 낮은 가중치의 간선을 선택하고, 신장 트리에 추가한다. 만약 해당 간선으로 사이클이 형성된다면, 신장 트리에 추가하지 않는다.
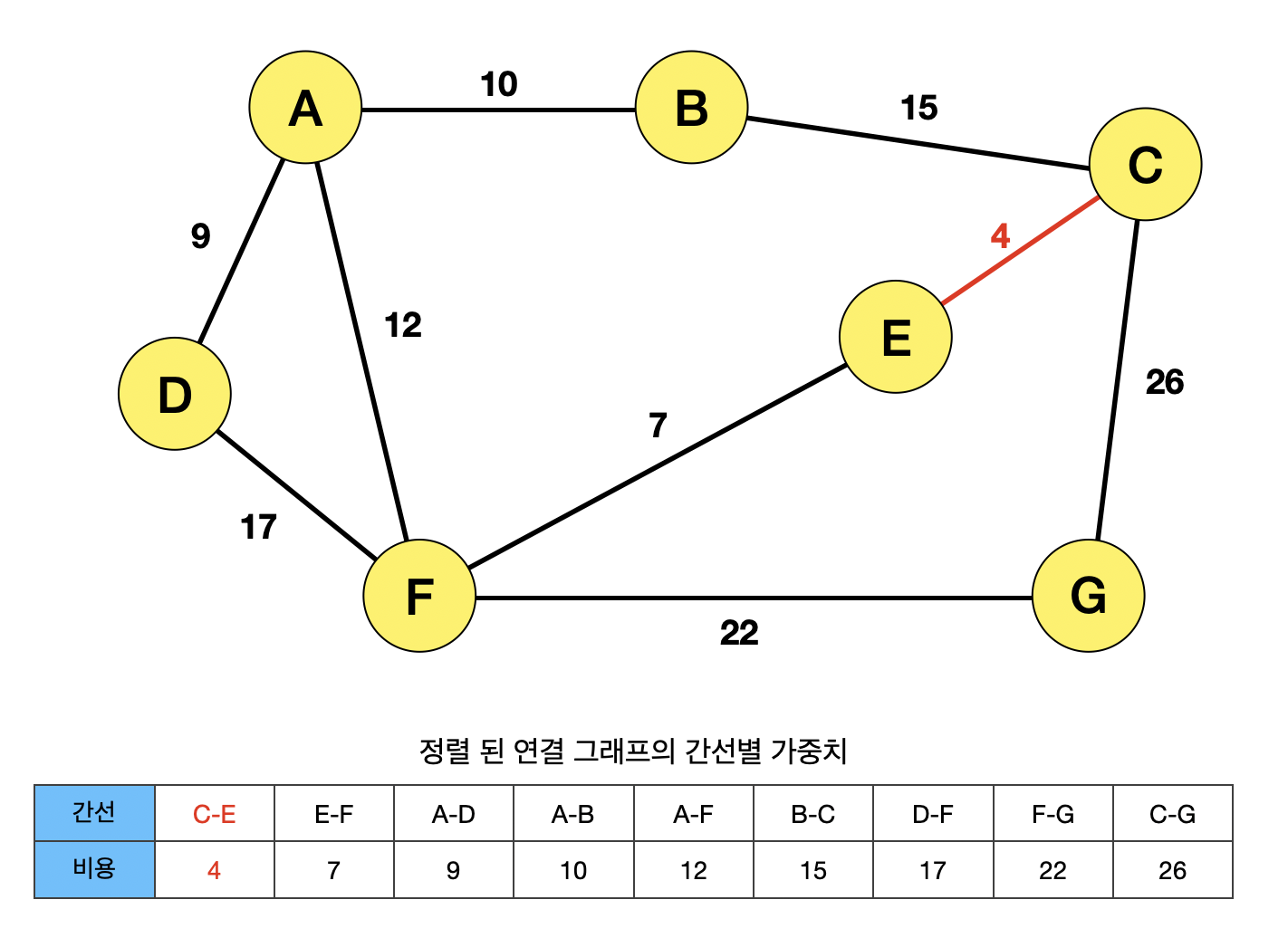
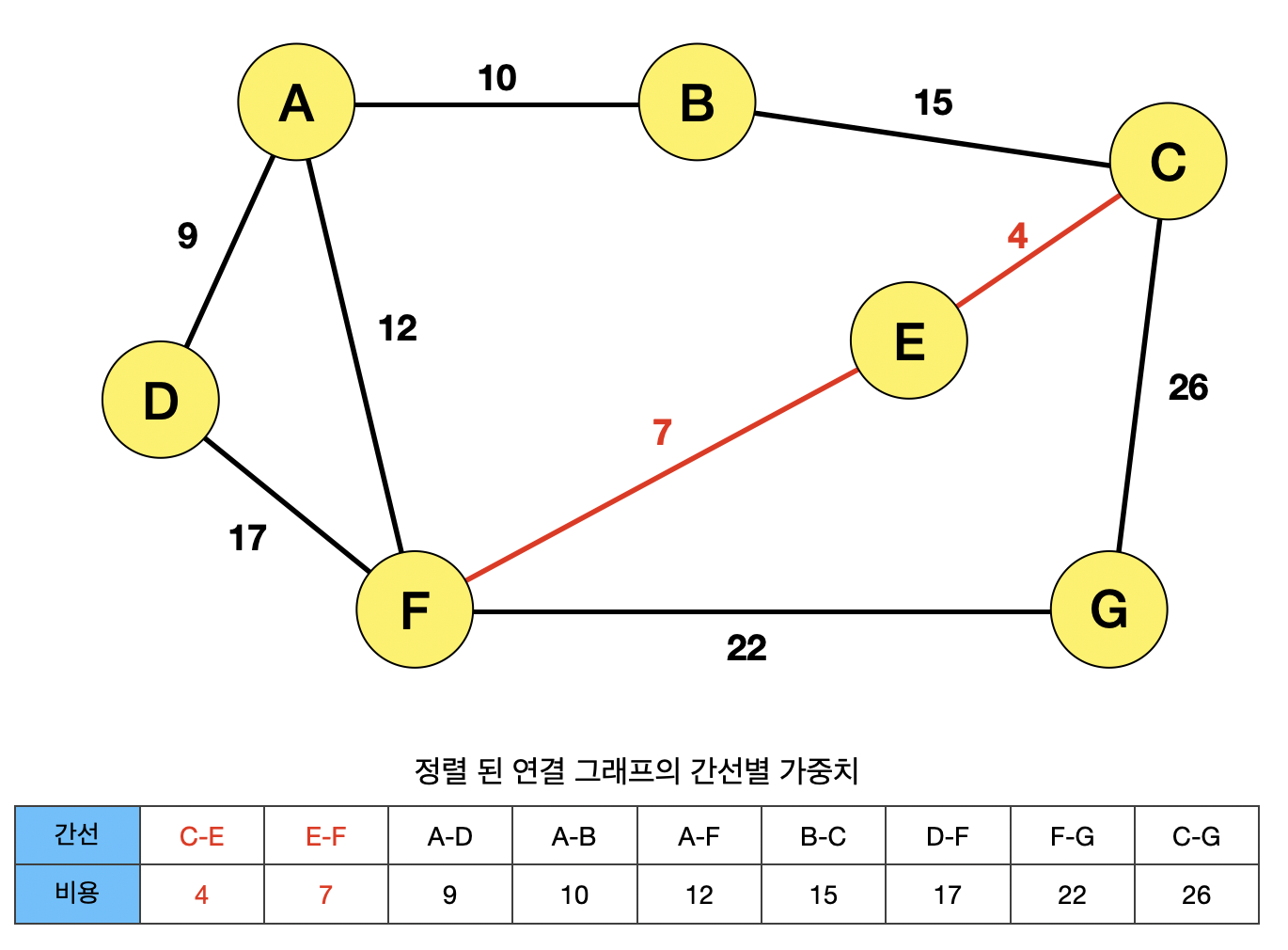
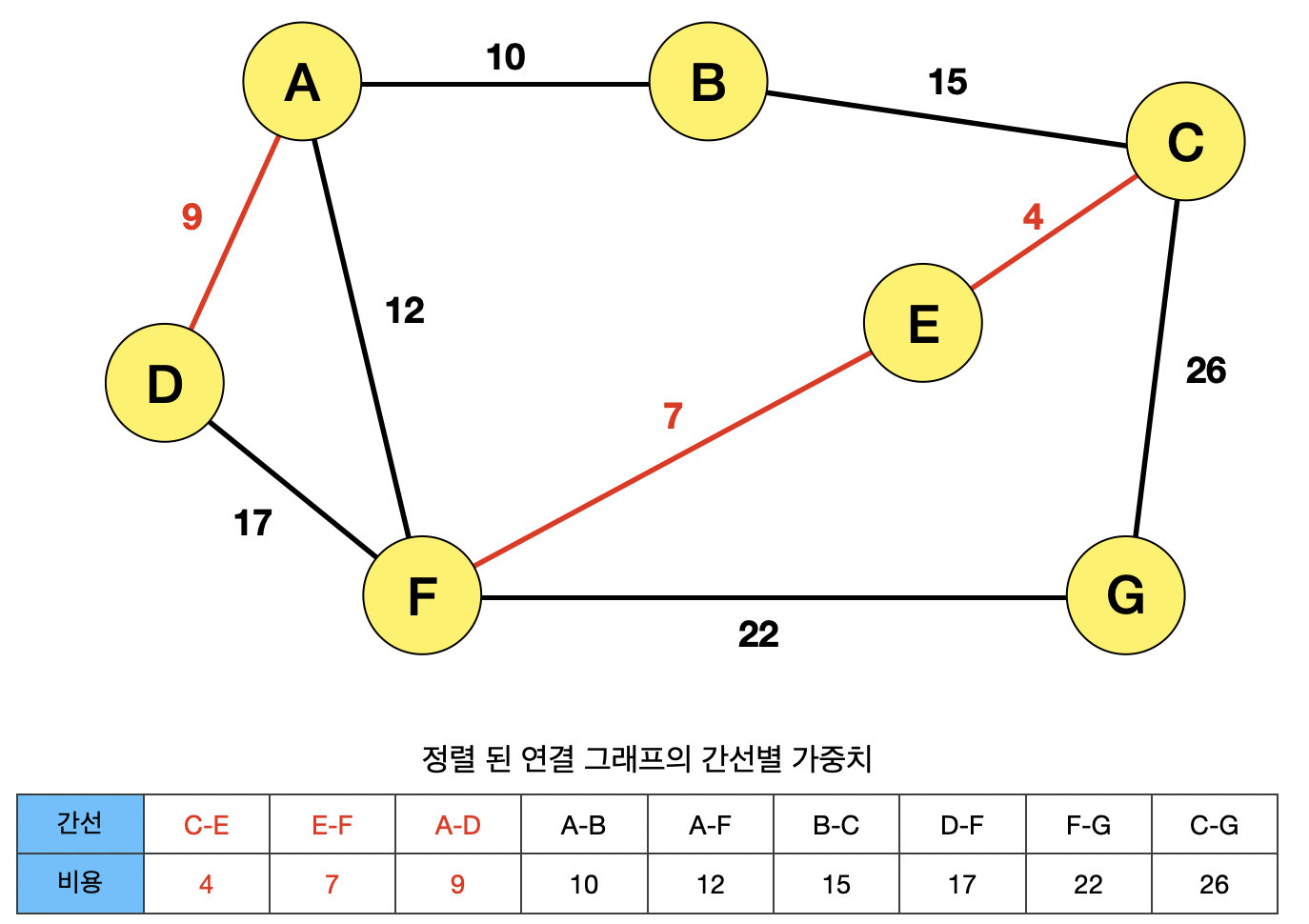
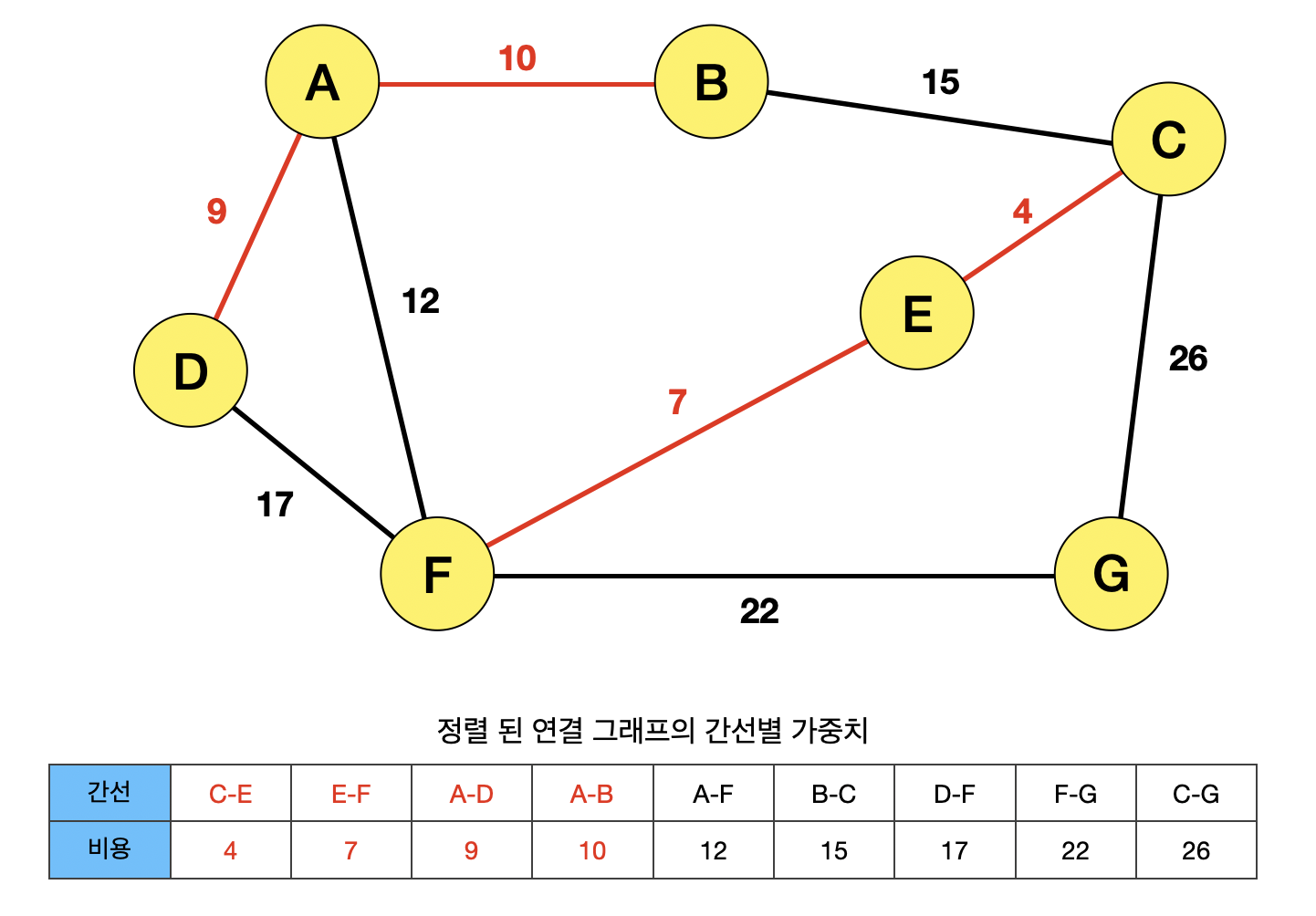
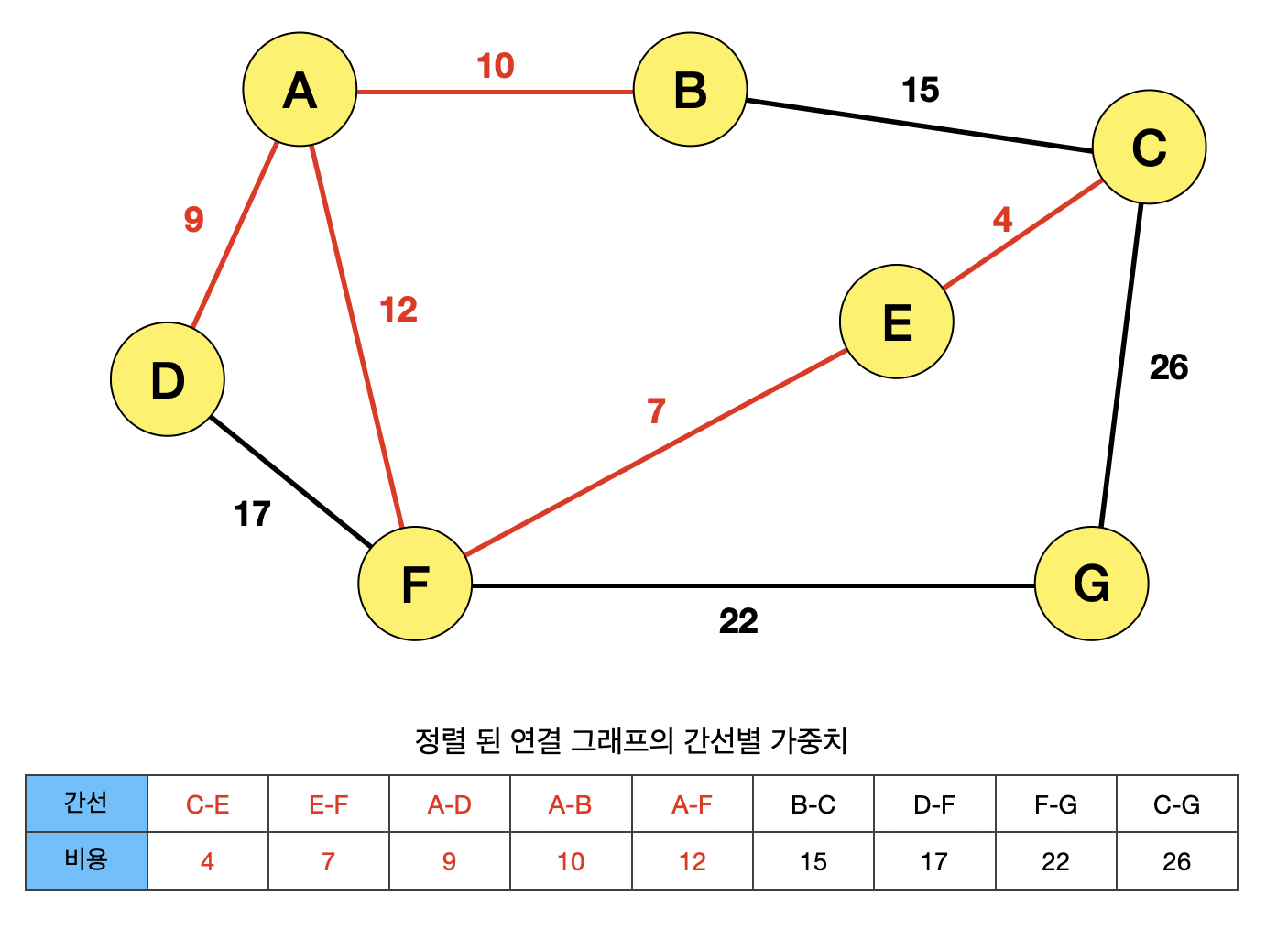
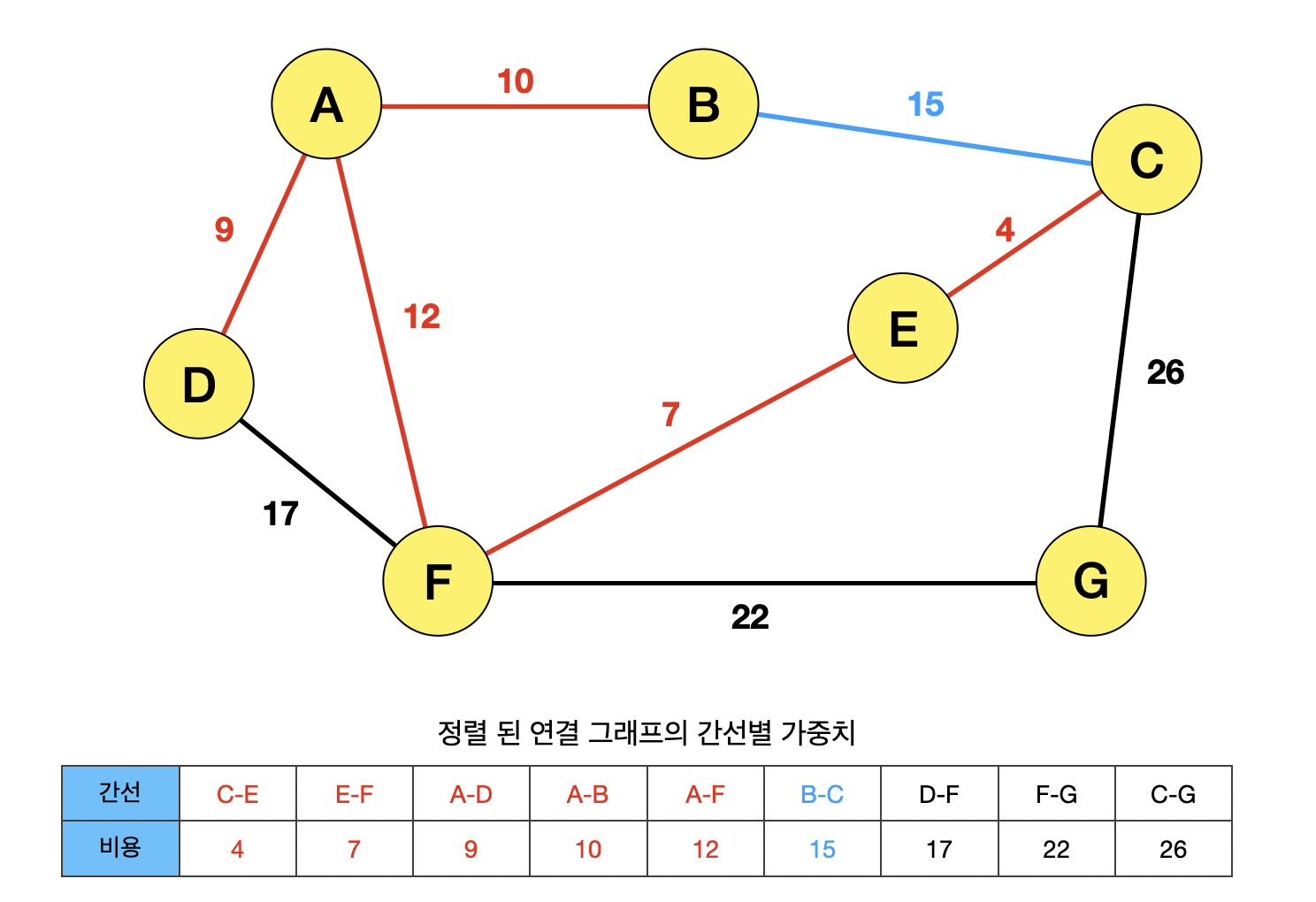
B와 C 사이의 간선이 선택되면서, ABCEF의 사이클이 생기기 때문에, 간선 BC는 선택될 수 없다.
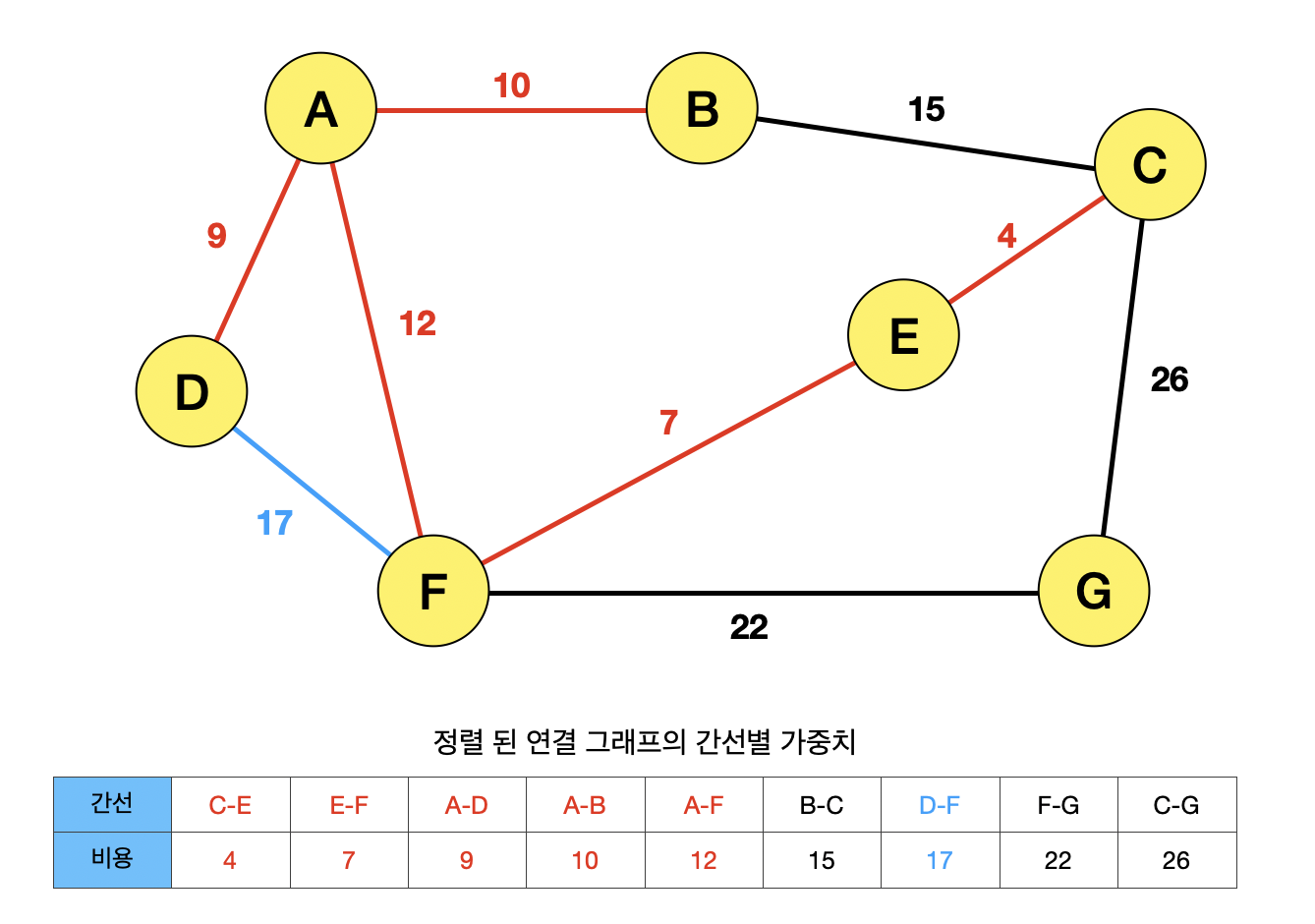
마찬가지로, DF 사이의 간선이 선택되면, ADF의 사이클이 생성되기 때문에 간선 DF는 선택될 수 없다.
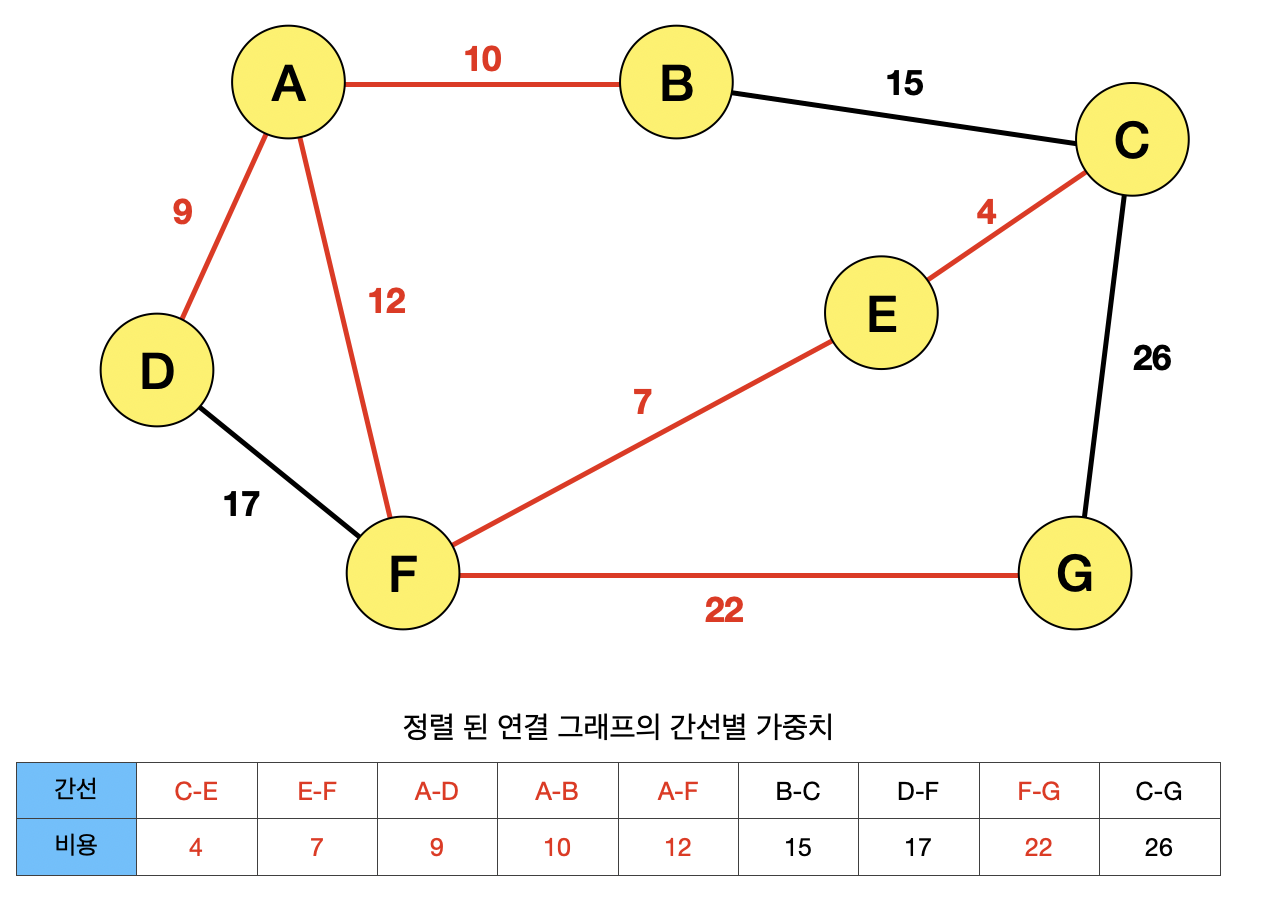
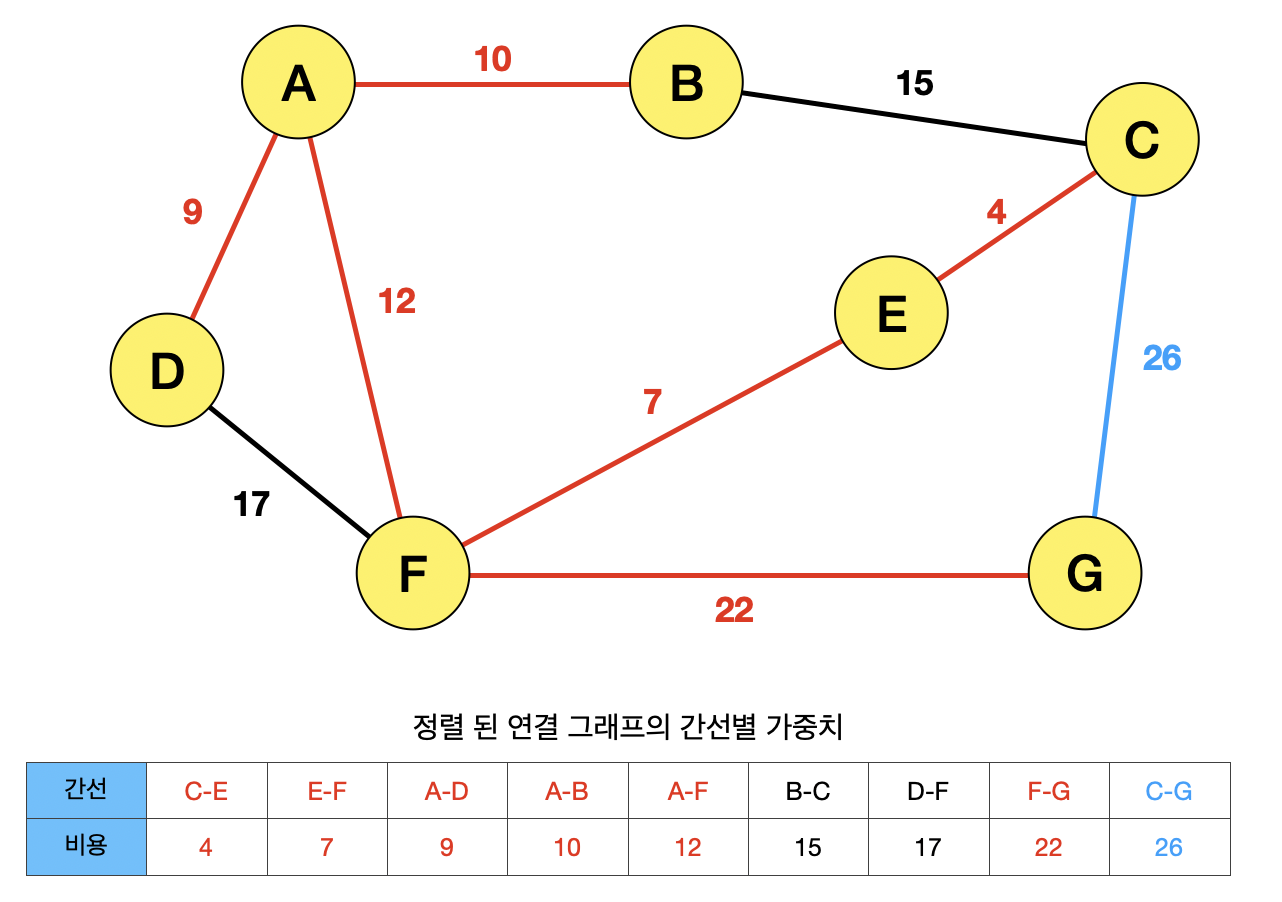
간선 CG가 선택되면, CEFG의 사이클이 생성되기 때문에 선택될 수 없다.
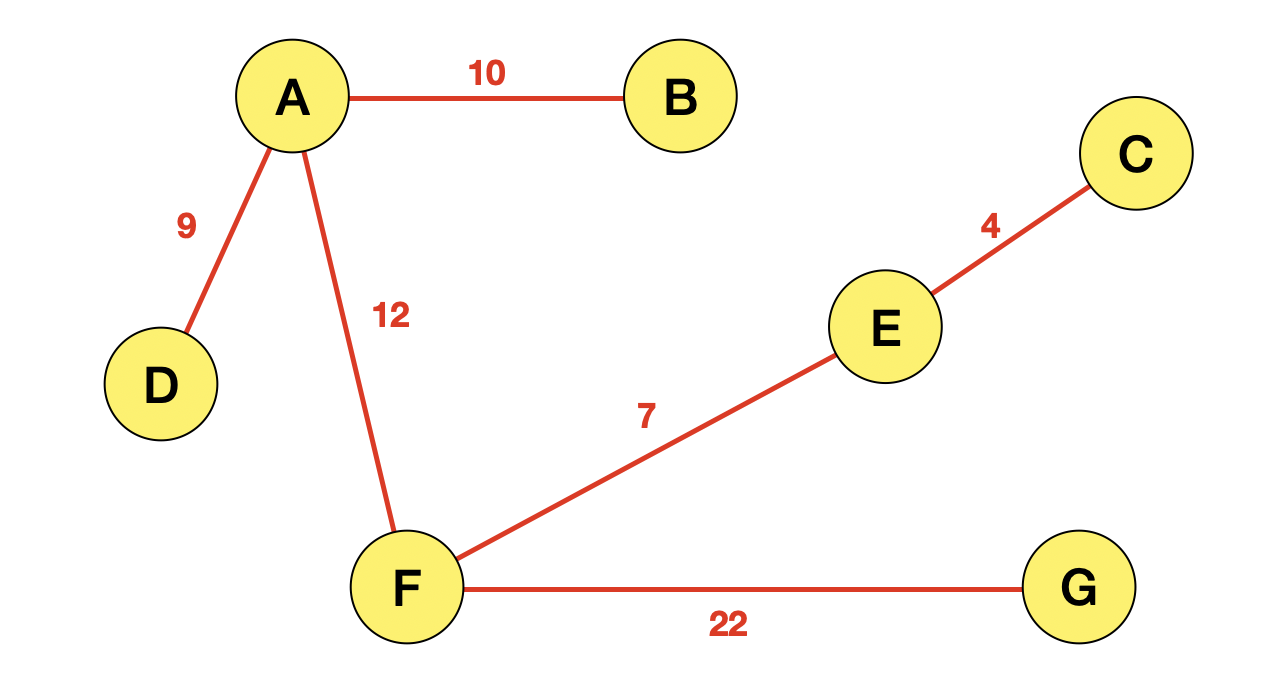
따라서, 총 비용이 64의 이러한 모양의 MST가 생성됨을 알 수 있다.
사이클 확인은 어떻게??
크루스칼 알고리즘의 과정을 살펴보면, 어느 한 간선을 선택했을 때, 해당 간선이 사이클을 형성하면 최소 신장 트리의 간선으로 선택하지 않는다는 조건이 있다.
어떻게 그래프에서 사이클이 형성되는지 알 수 있을까?
간선을 선택했을 때, 간선이 잇고 있는 두 노드를 Union 하고, 두 노드가 같은 집합에 속해있다면 사이클이 있다고 판단한다.
서로소 집합(Disjoint Set, Union-Find)을 이용하면 쉽게 사이클을 판별할 수 있는 것이다.
서로소 집합에 대한 이해는 여기에서 확인할 수 있다.
동작방식 with Union-Find
그럼, 앞서 소개한 예시에서, Union-Find 알고리즘을 적용해보자.
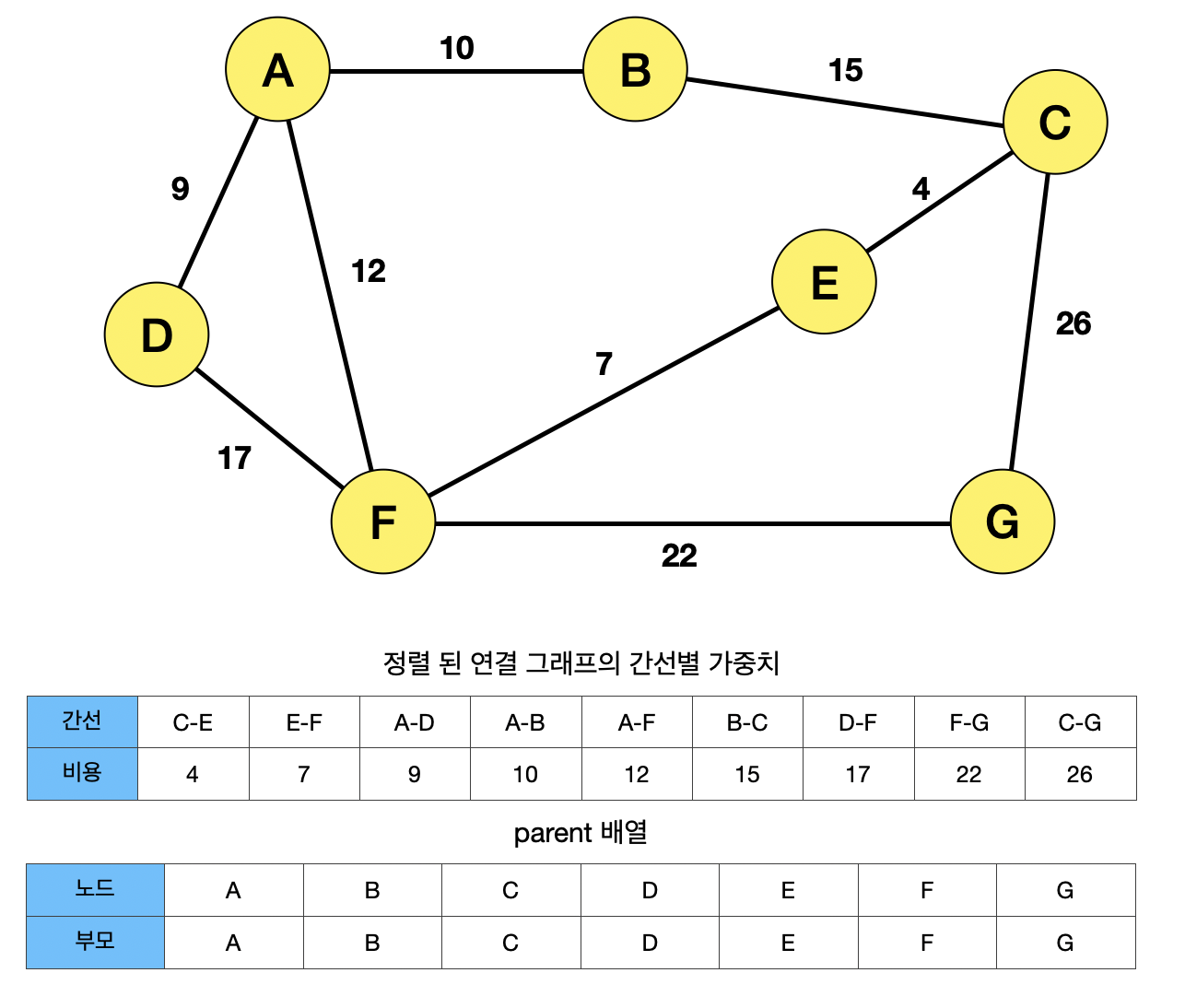
MakeSet 연산으로, 모든 노드의 부모는 자기 자신으로 초기화 되어있다.
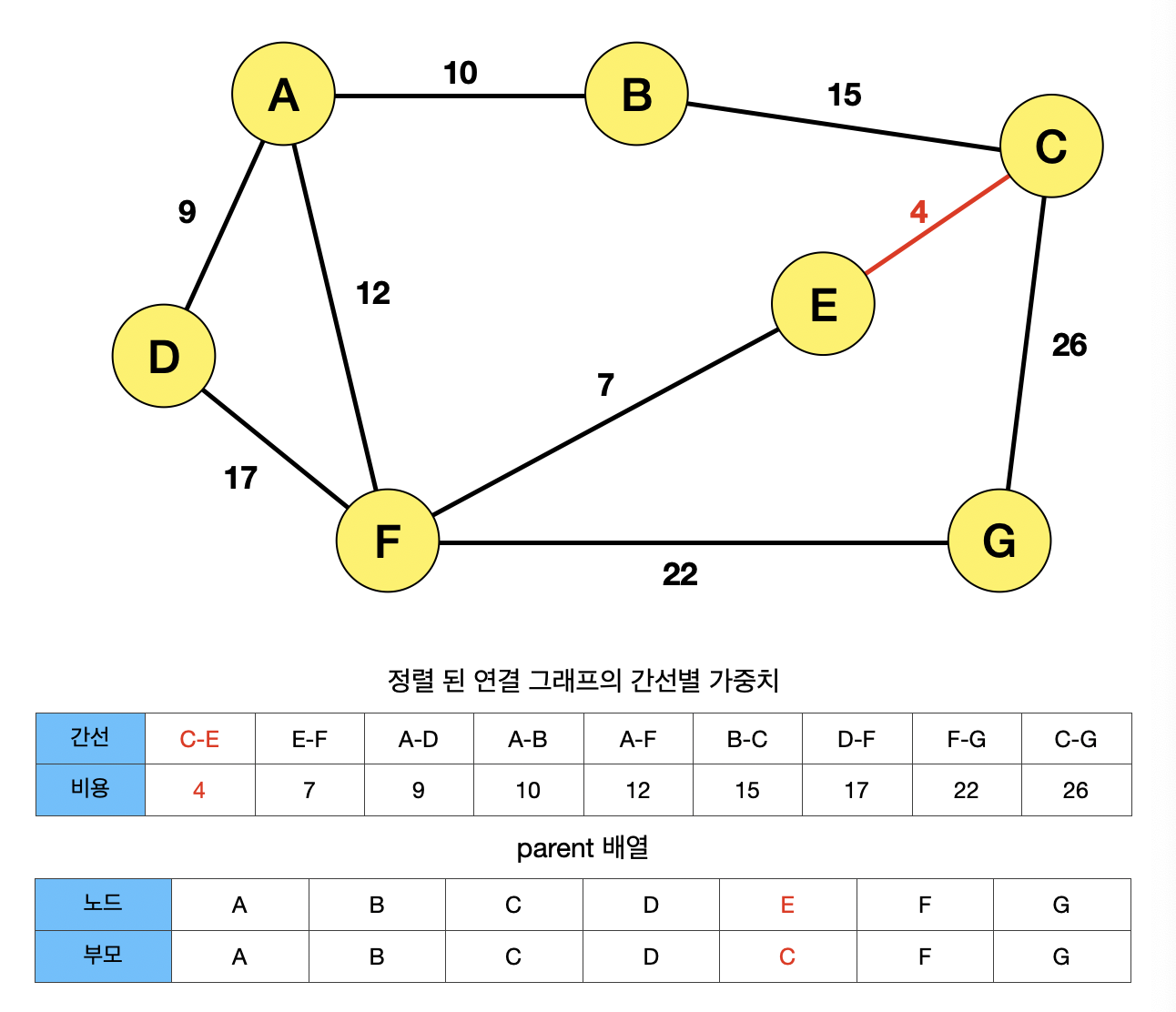
마찬가지로, 비용이 가장 낮은 간선 CE를 선택하고, 노드 C,E에 대하여 Union-Find 알고리즘을 적용한다. Union 연산을 할 때, 알파벳이 작은 순서를 가리킨다고 가정하면, 노드 E는 노드 C를 가리키게 된다.
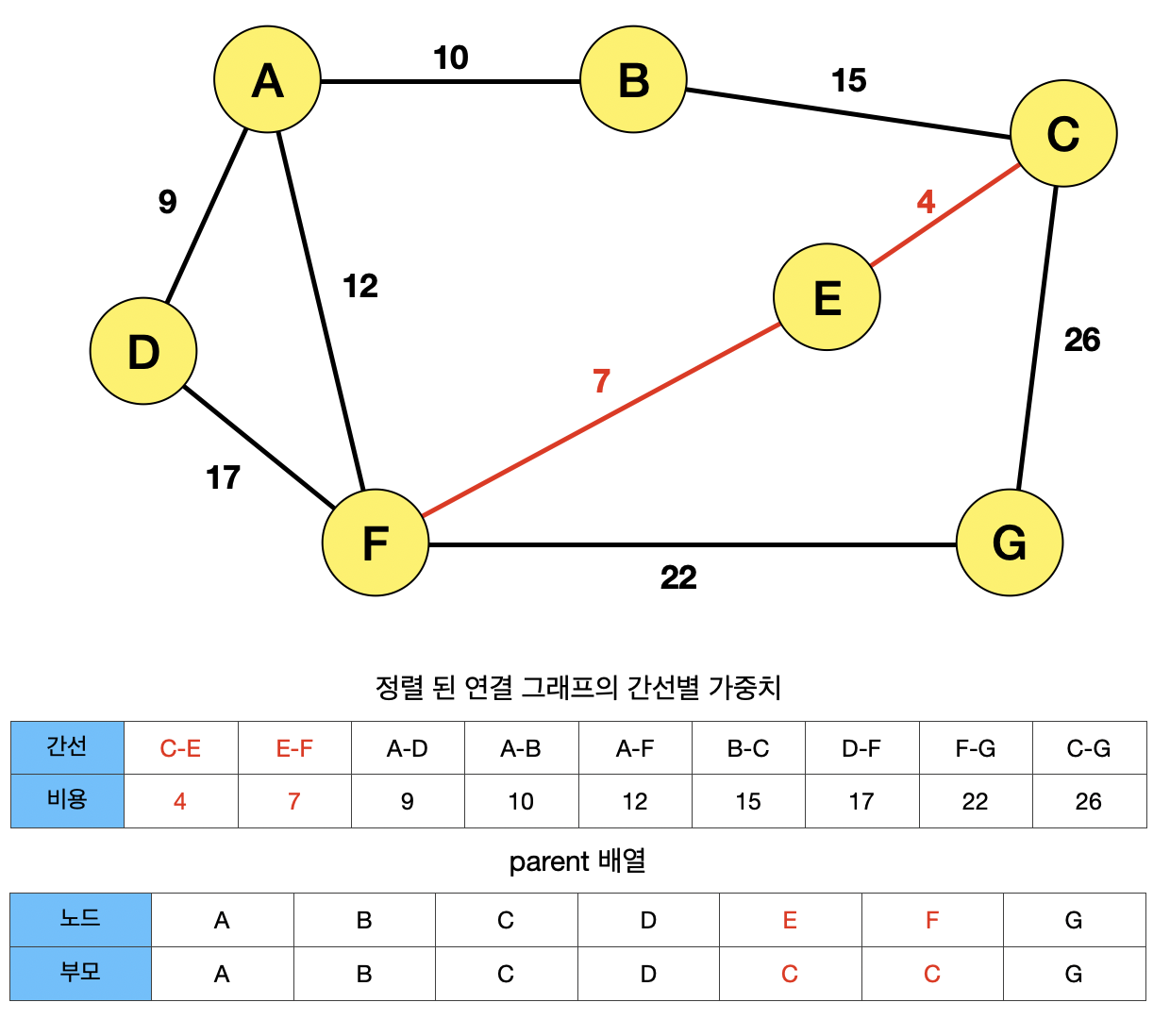
간선 EF가 선택되고, 노드 E와 F에 대하여 Union-Find 알고리즘을 적용시키면, F의 부모가 E의 최고 부모 C로 Union 된다.
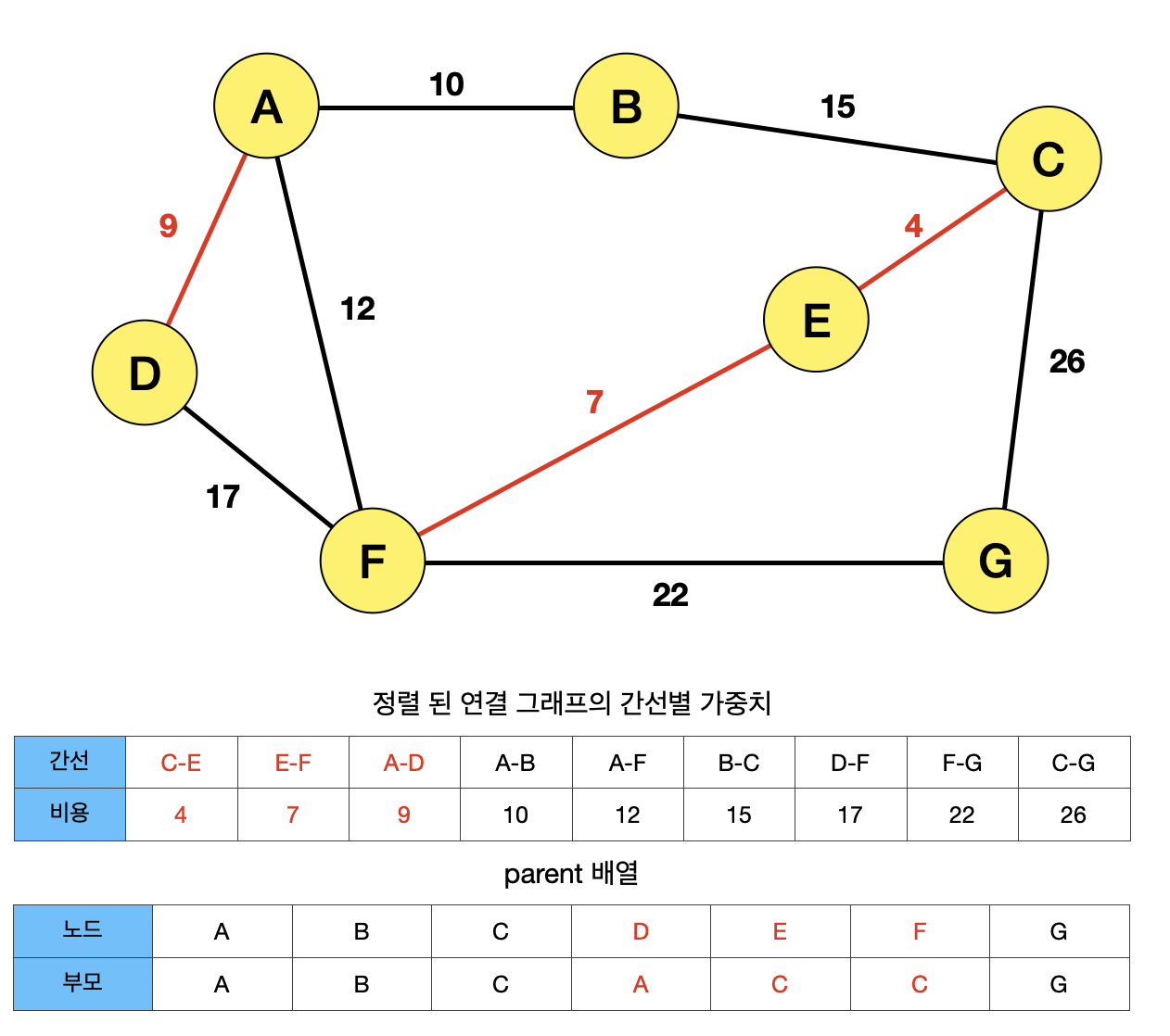
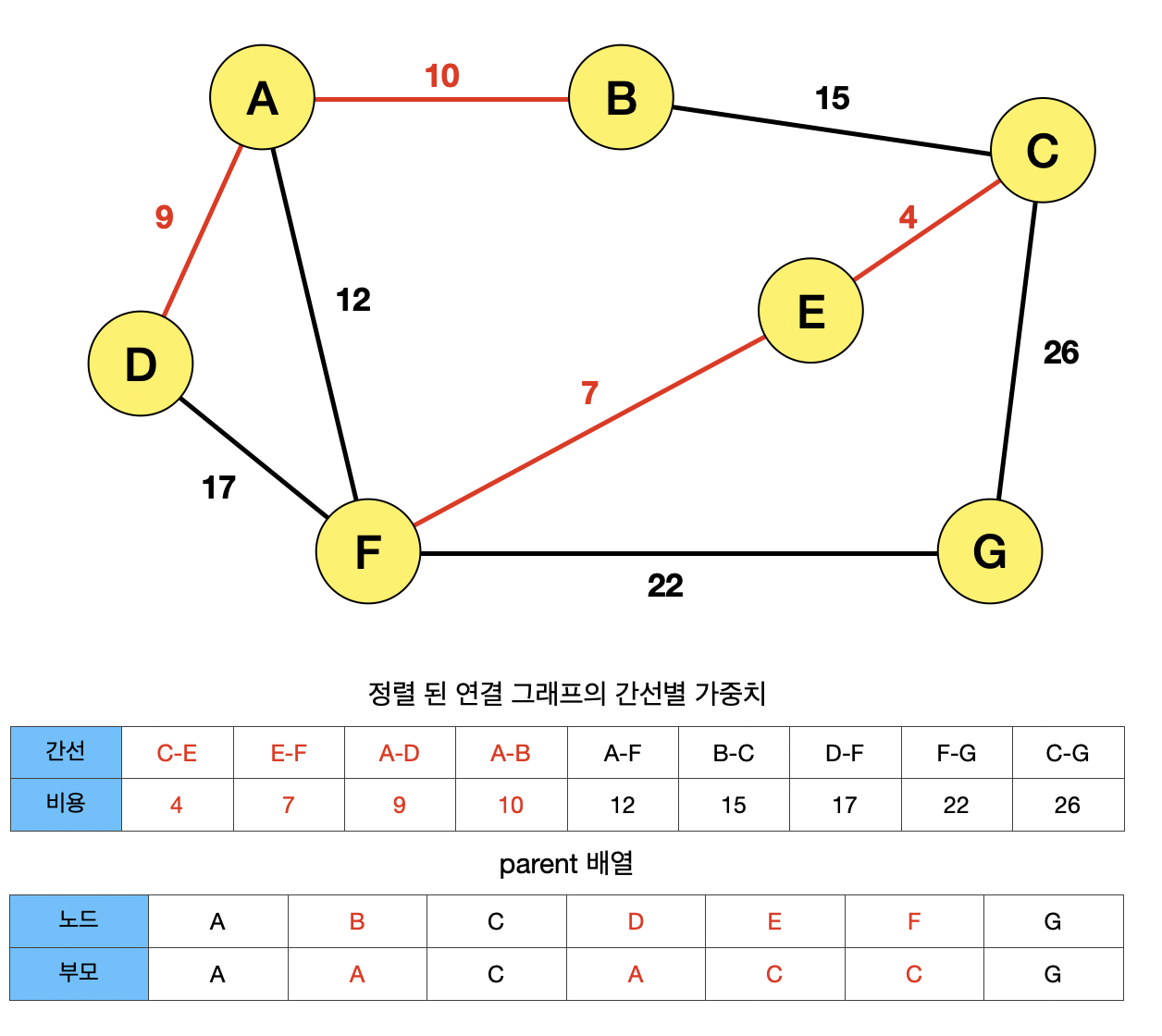
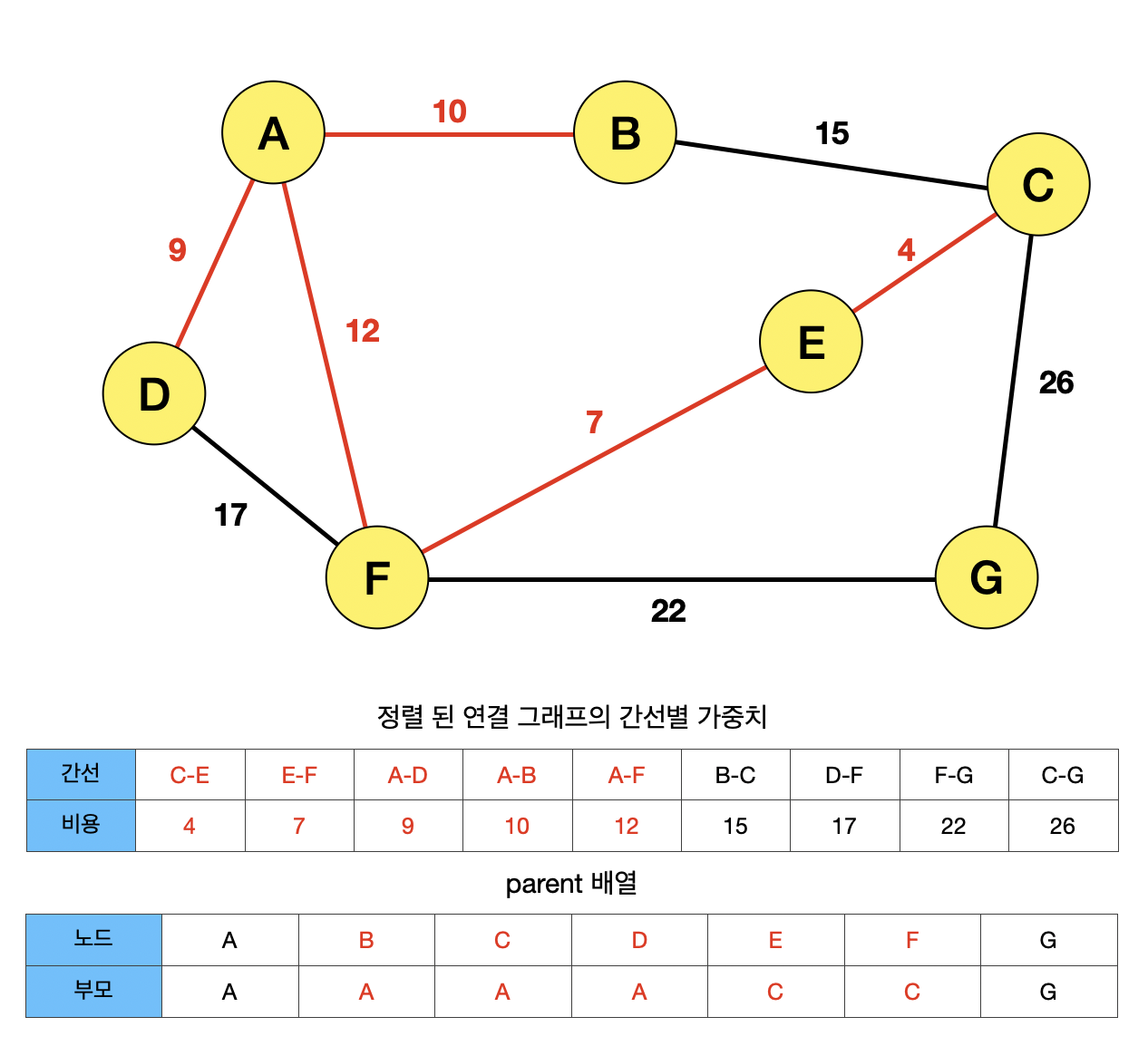
간선 AF가 선택되면서, 노드 A와 F가 Union하게 된다. F의 최고 부모 C가 A보다 크기 때문에, C의 부모가 A로 변경되게 된다.
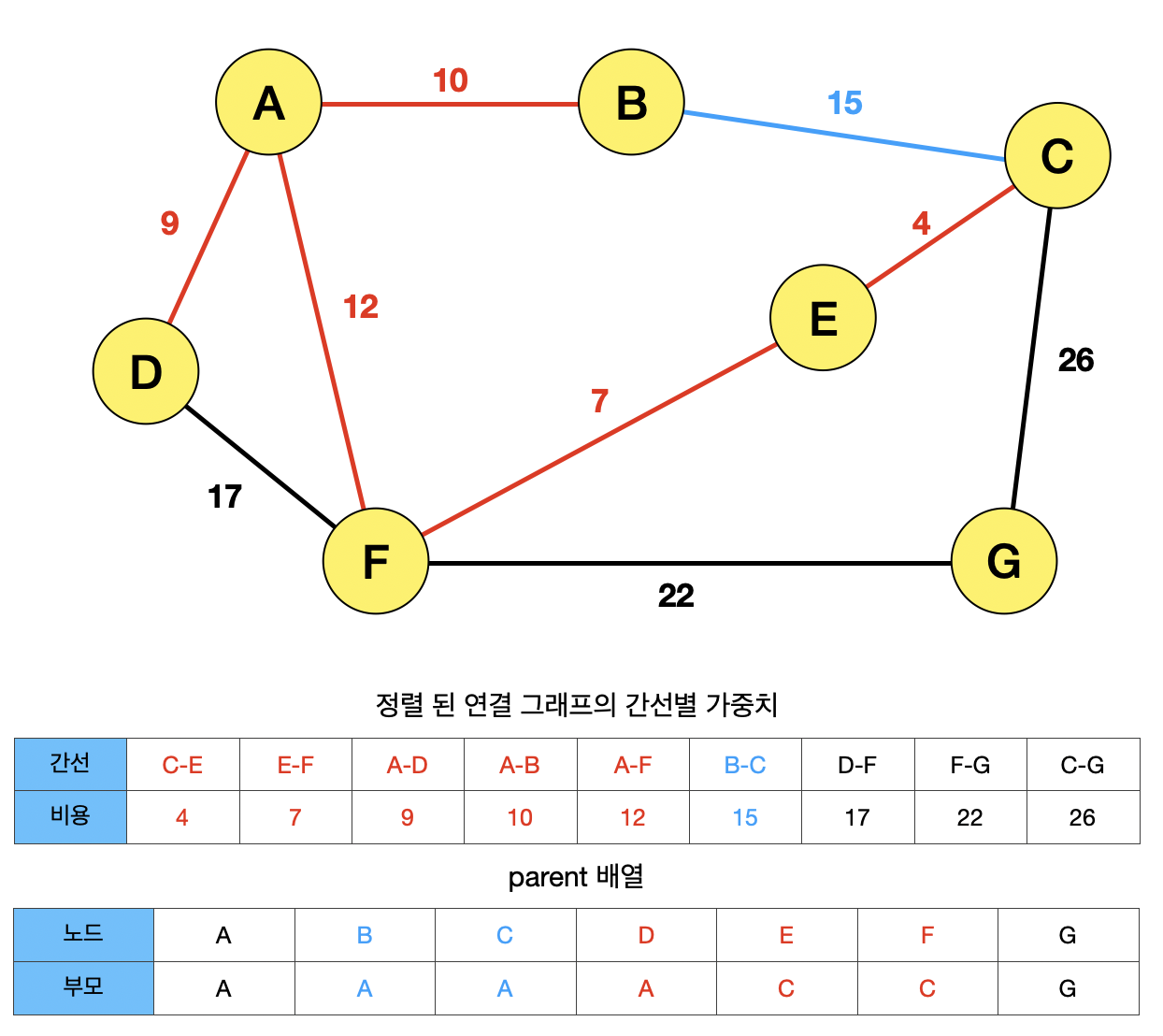
간선 BC가 선택되고, 노드 B와 C를 find 연산하면, B와 C가 같은 노드를 부모로 갖고 있으므로, 사이클이 형성되어 선택될 수 없다.
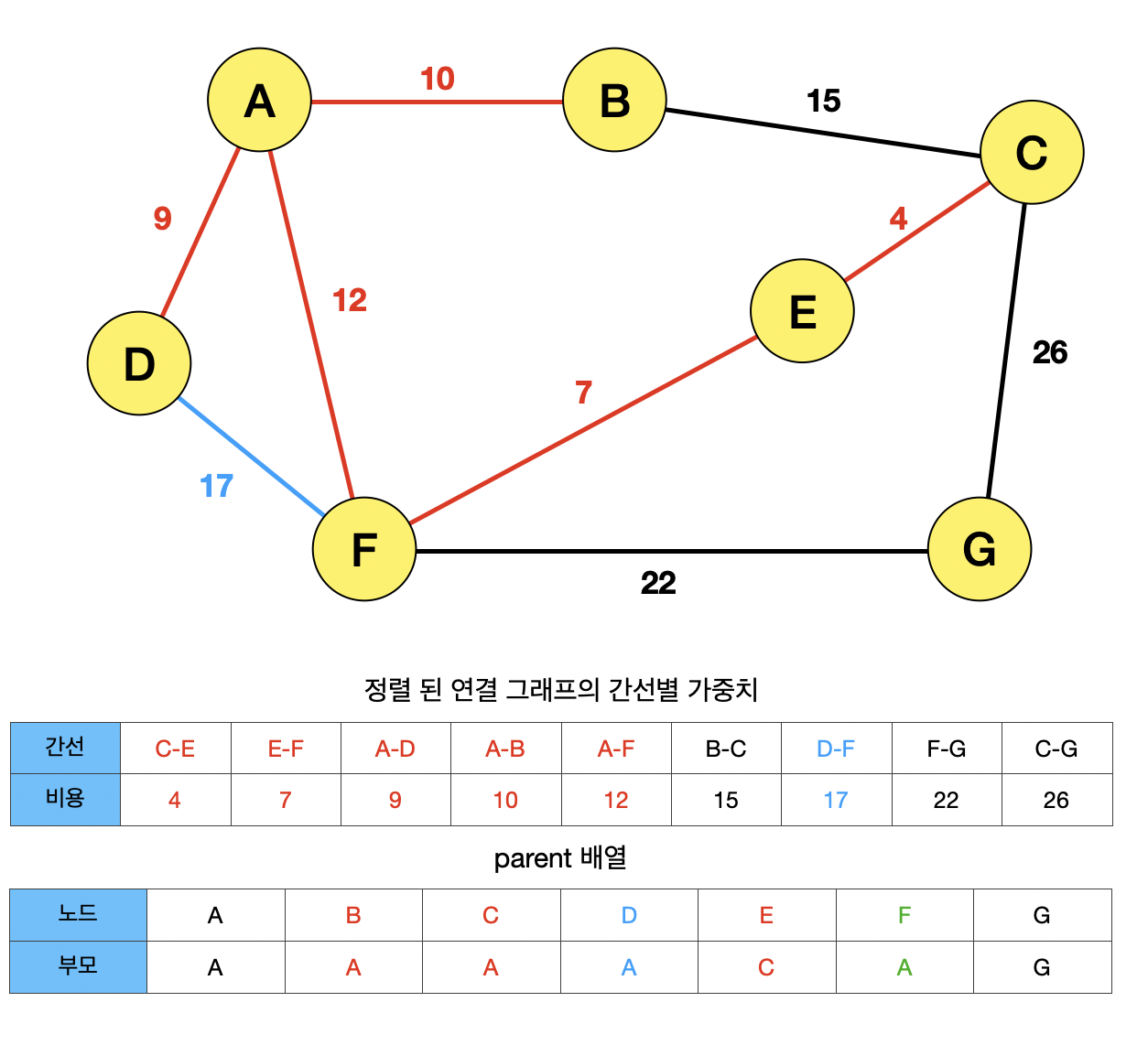
간선 DF가 선택되고, 노드 D와 F가 find 연산을 수행하게 된다. F를 find 연산하면, 기존의 최고 부모 C에서, 갱신된 최고 부모 A로 값이 변경된다. 이에 따라 노드 D와 F의 부모가 같으므로 사이클이 형성되어 선택될 수 없다.
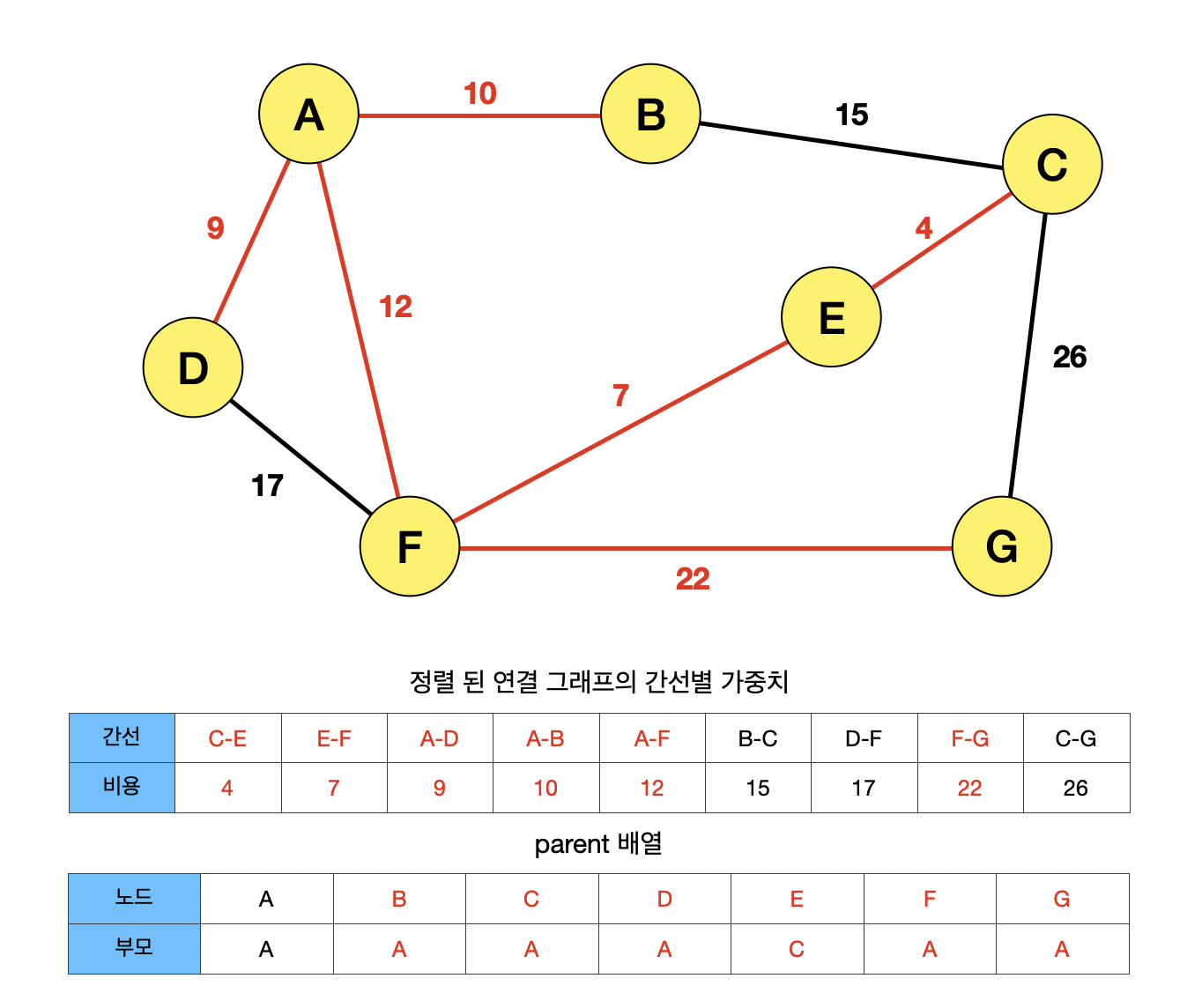
간선 FG이 선택되면서, 노드 F와 G가 Union 연산으로 부모값이 A로 지정된다.
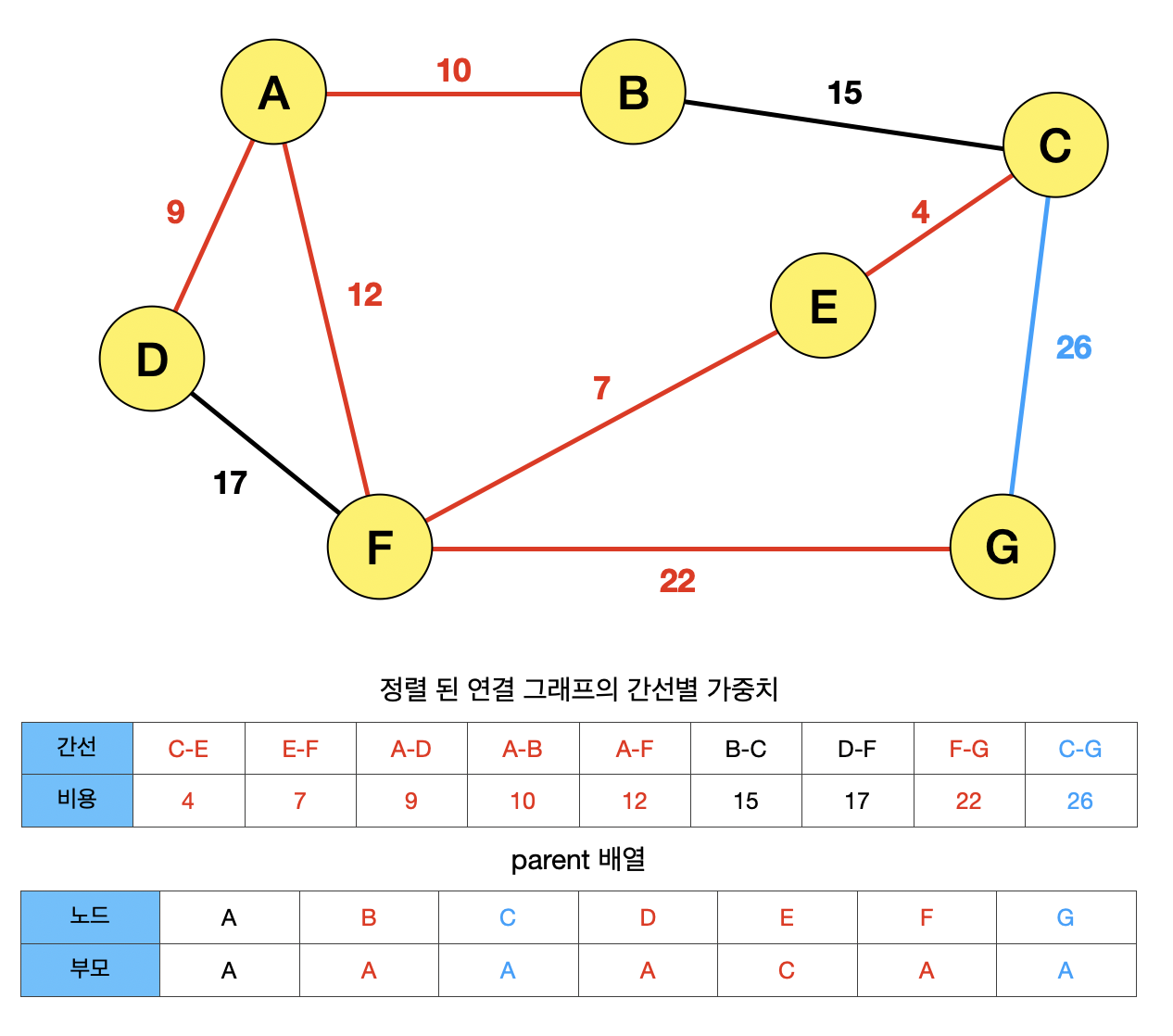
마지막으로, 간선 CG를 선택하면 노드 C와 G의 find 연산 한 값이 A로 동일하므로 MST 간선으로 선택될 수 없다.
예제 문제
백준 온라인 저지의 1197번 최소 스패닝 트리문제를 예시 문제로 제시하고, 마무리 하겠다.
<<문제>>
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.<<입력>>
다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다.
이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다.
C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다.
최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고,
2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.<<소스 코드>>
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Baek_1197_Kru {
static int[] parents;
public static void main(String[] args)throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System. in));
StringTokenizer st = new StringTokenizer(bf.readLine());
// 1. 모든 간선을 가중치를 기준으로 오름차순 정렬한다.
PriorityQueue <int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
@Override public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
int v = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
parents = new int[v + 1];
for (int i = 1; i <= v; i ++) {
parents[i] = i;
}
for (int i = 0; i < e; i ++) {
st = new StringTokenizer(bf.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
pq.offer(new int[]{a, b, c});
}
long answer = 0;
while (!pq.isEmpty()) {
int[] poll = pq.poll();
int p1 = poll[0];
int p2 = poll[1];
int dist = poll[2];
// 만약 해당 간선으로 인해 사이클이 형성 된다면, 해당 간선을 무시한다.
if (find(p1) == find(p2))
continue;
// 가장 낮은 가중치의 간선을 선택하고, 신장 트리에 추가한다.
answer += dist;
union(p1, p2);
}
System.out.println(answer);
}
static int find(int x) {
if (parents[x] == x) {
return x;
} else {
return parents[x] = find(parents[x]);
}
}
static void union(int x, int y) {
x = find(x);
y = find(y);
if (x > y) {
parents[x] = y;
} else {
parents[y] = x;
}
}
}- 첫번째로, 모든 간선을 가중치를 기준으로 오름차순 정렬한다.
- 가장 낮은 가중치의 간선을 선택하고, 신장 트리에 추가한다. 만약 해당 간선으로 인해 사이클이 형성 된다면, 해당 간선을 무시한다.
- 위 과정을 모든 노드에 닿을 때까지 반복하면, 최소 신장 트리가 만들어진다.
코드가 복잡해보일 수 있지만 앞서 언급한 세 단계의 동작 방식을 생각한다면 쉽게 이해할 수 있다.
참고로 필자는 모든 간선의 가중치를 오름차순 정렬하여 이용하기 위해 우선순위 큐를 사용하였다.



